
By Thibault Groueix (École des Ponts, Adobe Research intern), Matthew Fisher (Adobe Research), Vladimir Kim (Adobe Research), Bryan Russell (Adobe Research), Mathieu Aubry (École des Ponts)
Computers have made significant progress in understanding what is depicted in images. For example, a computer can often correctly recognize whether an image contains a cat or dog, and more recently computers have shown an impressive capability to generate images.
How about for 3D? We live in a 3D world, and a “holy grail” in computer vision is for a machine to generate information about the 3D world starting from a single image. At the moment, it’s an open challenge for a computer to learn how to generate high-resolution 3D shapes.
Generating 3D shapes is difficult as they lack a “natural” parameterization, meaning there is no order to 3D elements. This difficulty is in contrast to 2D image pixels, which have a natural ordering based on a pixel grid and allow convolutional neural networks to operate over the grid.

Figure 1. Our approach outputs a 3D polygonal mesh given an input image. We can also 3D print the depicted shape.
In our work, “AtlasNet: A Papier-Mâché Approach to Learning 3D Surface Generation,” which will appear at the Conference on Computer Vision and Pattern Recognition (CVPR) 2018, we show how to generate a 3D polygonal mesh automatically starting from a single 2D image using a neural network. Polygonal meshes are a standard way to represent virtual environments in video games, movies, and CAD models. We introduce a novel approach for generating 3D polygonal meshes with a neural network yielding high-fidelity 3D reconstructions, which is vital for 3D content generation.

Figure 2. Output voxel and point-cloud representations for the input image shown in Figure 1.
To provide some context for our work, we will briefly summarize two different ways neural networks have primarily generated 3D shapes before our work: (i) outputting a voxel-based representation, and (ii) outputting a point cloud-based representation. A voxel is a 3D analog to a 2D pixel — instead of having a 2D grid of pixels covering an image, you have a 3D grid of voxels covering 3D space. Figure 2 (left) shows an example of an output voxel representation for a 3D shape. Voxel outputs may look blocky, and getting high-resolution outputs is a challenge. Generating high-resolution outputs requires higher sampling of the voxel grid, which increases memory usage. Recent work has looked at producing higher fidelity outputs by concentrating more voxels at the shape’s surface. In contrast, a point cloud representation encodes a 3D shape via a set of 3D points sampled on the shape’s surface. Figure 2 (right) shows an example of a point cloud representation for a 3D shape generated by a neural network. One drawback for 3D points is we do not know explicitly if nearby points are on the same surface, which is important for applications in computer graphics, such as texture mapping.
In our work, we seek to overcome the limitations of voxel-based and point cloud-based representations by generating directly a 3D polygonal mesh. A polygonal mesh consists of a set of 3D points (also known as vertices) and a connectivity structure over the 3D points (for example, triangles or quadrilaterals) indicating the shape’s faces. The faces may also have a set of 2D coordinates (also known as UV coordinates) which can be used to apply a texture map.
Our goal is for a neural network to generate a polygonal mesh representation directly given an input image. Figure 1 shows an example mesh generated by our neural network.
In a nutshell, our approach learns how to map a set of 2D patches to the surface of a 3D shape, which is a key novelty of our work. You can think of this as similar to your elementary school art class when you created a papier mâché. A papier mâché is formed by first placing strips of paper in glue and then covering a 3D shape with the paper strips.
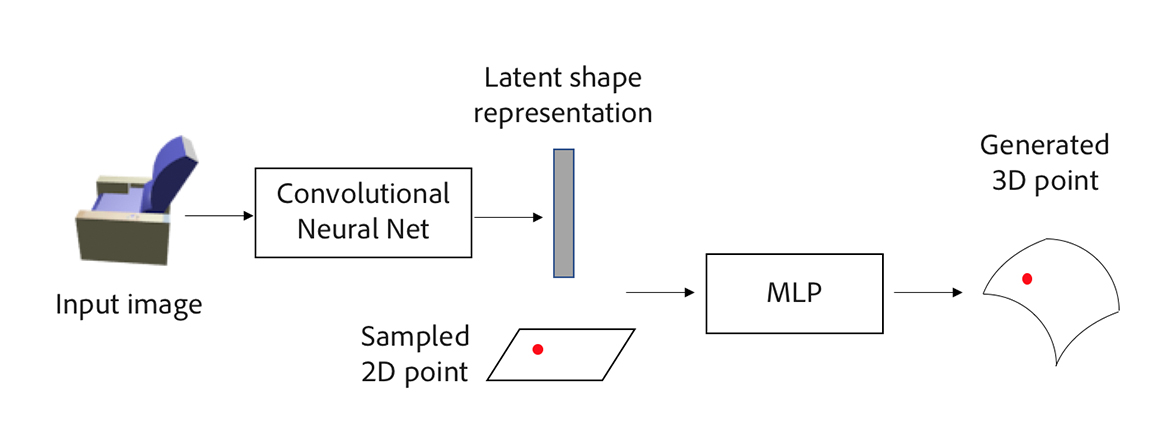
Figure 3. Overview of our approach for a single patch.
For a computer to create a papier mâché for a depicted shape in an image, we first pass the input 2D image through a convolutional neural network to yield a feature vector representation of the 3D shape. Next, we sample a 2D point on a 2D patch (our “paper strip”). The feature vector and sampled 2D point are passed through a second neural network consisting of a multilayer perceptron (MLP) with ReLU nonlinearities, which generates a 3D point on the shape’s surface. We can generate more 3D points by sampling more 2D points on the 2D patch and repeating the same procedure. Figure 3 illustrates our approach for a single patch. Note that we may incorporate more “paper strips” by sampling points on multiple 2D patches and then passing them along with the feature vector representation through multiple MLPs. We train our model using a large corpus of 3D shapes along with rendered views of the shapes.
So far, we have generated a set of 3D points for the shape. How do we get the 3D shape’s faces? We show in the paper that each MLP maps a local neighborhood around each point on the 2D patch to a local surface on the 3D shape. This property allows us to define a set of faces for the generated 3D points via a connectivity structure (for example, triangulation) over the sampled 2D points on the patch. Note that our approach can also take as input a 3D shape, such as a 3D point cloud, for 3D surface reconstruction. Please see our paper for more details.

Figure 4. Applying texture to our generated mesh.
The ability to generate polygonal meshes opens up many applications. For example, we can view the 2D sampled patches as an atlas of the 3D shape, which allows us to apply textures on the shape. If we minimize distortion on the inferred atlas, we can apply a texture directly as shown in Figure 4.
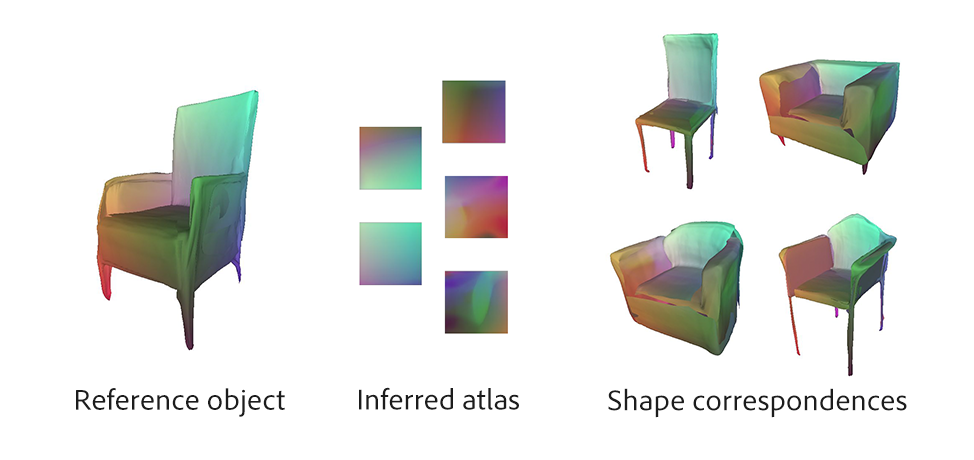
Figure 5. Shape correspondences.
One feature of our learned approach to mesh generation is that the neural network appears to learn shape correspondence implicitly. As seen in Figure 5, if we color each 2D patch and apply these colors across different shapes using the texture mapping procedure above, we can see that the network implicitly colors similar semantic parts consistently. For example, the front chair legs and chair seat have consistent colors.

Figure 6. 3D shape morphing.
Finally, we show some fun visualizations of morphing between two different 3D shapes in Figure 6. To produce the shape morphing, we smoothly transition from one feature representation of a 3D shape to another and generate the output 3D mesh. Notice how the intermediate shapes gradually add and subtract parts.
In summary, we have introduced a new approach for generating 3D data, which could have an impact beyond the scope of the applications mentioned above. Our work is an effort in the direction of fast and easy acquisition of high-quality 3D data from a single image or point cloud inputs from a depth/range scanner. The ability to easily acquire 3D data could potentially impact many areas. For example, 3D assets are heavily used in movies, video games, and architectural design. A more extensive library of 3D shapes could allow artists to more easily create richer environments. We also imagine that scanned 3D objects or environments will enable users wearing a virtual/augmented reality headset to insert and view new furniture in their own home or to view changes of a factory for industrial/facility maintenance applications.
For more details of our approach and to view more results, please see our project webpage and paper.