Part 2: Patch-Based Synthesis

by Aaron Hertzmann, Adobe Research

This is the second blog post in a series of three posts on the history of image stylization algorithms. The first post is here, and the final post is here.

In this article, I’ll cover patch-based methods for example-based image stylization. In science and academic research, many investigations lead to surprising connections. Here is one example: All of our modern stylization methods arose from research into the seemingly-different problem of visual texture recognition. (There had previously been inspirational work on style-content separation with bilinear models, and our own work on time-series models, but these did not generalize to natural images.)

The Texture Perception Problem

The visual texture recognition problem is this: given an image of a piece of wood or a vine-covered wall, etc., can a computer recognize what texture it is? We, as humans, are able to do so, even if we’ve never seen that particular bit of wood grain or pattern of vines before. This led Bela Julezs, a psychologist studying human vision, to hypothesize in the 1960’s that human texture recognition must be based on image statistics in some way: it relies on aggregate distributions rather than recognizing specific arrangements of pixels.

Early texture recognition methods in the 1970s counted statistics of neighboring pixel values, e.g., what percentage of dark pixels lie next to other dark pixels. Such methods could only model very simple patterns, and they were sensitive to overall lightness and darkness in ways that humans are not. Researchers also knew that the human vision system uses multiscale edge- and orientation-selective filters (i.e., oriented derivative filters), which are often invariant to lighting, while also capturing longer-range structures. Hence, they attempted to model the statistics of these filter responses. This gave better recognition scores, but how could researchers gain some understanding for how their models were working?

One way to test a texture perception model is to synthesize texture from it: generate a random new image with the same statistics of the model, as suggested by Heeger and Bergen. Portilla and Simoncelli described a very sophisticated texture representation involving joint statistics of the outputs of many different image filters, inspired by human perception (and, in retrospect, like a 2-layer convolutional model). Their method produced intriguing results that, at first glance, looked very much like the textures they were mimicking, capturing various large-scale structures. On closer inspection, however, their method still fused structures together in unnatural ways. Moreover, their method was very involved and slow (for the computers of the time), making it hard for other people to use.

Patch-Based Texture Synthesis

A very simple alternative was invented by Alyosha Efros, then a PhD student who, like me, was also left alone by his indulgent advisor. His method, developed together with Thomas Leung, is based on image patches: a patch is simply a square grid of pixels in an image, say, a 5×5 or 19×19 square cut out of the image. In its simplest form, his theory is that two images have the same texture if every patch in one image “looks like” a patch in the other image. For example, here are two photographs of a wooden surface. Even though the photographs have different pixel intensities, they appear to be of the same texture. And if we pick any small square patch of pixels in one image, we can find a patch in the other images that is very similar.

In this view, texture is anything that you can “rearrange” without changing the content of the image. Efros and Leung then described a very simple procedure for texture synthesis with this method. Starting with an empty image, their algorithm fills in pixels one-by-one, randomly sampling new pixels from the input texture, such that each new patch of filled-in pixels is always similar to some patch in the input image. (As with all the papers that I’m describing here, you can find a more detailed description in the paper itself.) Here’s one example of the results they achieved:

This algorithm is extremely simple to implement, and seems like magic: I remember thinking that I would never have believed it works had I not seen the results. And, yet, the results were often better than those of Portilla and Simoncelli’s very complex algorithm.

Since then, many improvements to this basic algorithm have been developed. The algorithm I described is both greedy and slow, and can fail in various cases. Notably, energy minimization methods address these problems by a joint optimization of all pixels to match some patch in the input texture, and PatchMatch (developed at Adobe and Princeton) a much better procedure for finding matching neighborhoods. Combining these methods gives a very fast and effective texture synthesis algorithm.

Image Analogies

A year after Efros’ paper was published, I was working on something very different when I realized that his method could also be adapted to image stylization.

My basic idea was as follows. Suppose we have a photograph, and, a hand-drawn illustration from that same image, e.g.:

These images are in pixel-wise correspondence, that is, each patch in A’ is lined up with a patch in A.

Now, suppose we want to produce a stylization of a new photograph in the style of that human artist. As in texture synthesis, I want every patch in the B’ image to look like some patch in the A’ image. However, I also want these patches to have the same relationship between the image pairs. For example, if each patch in A’ has the same low-frequencies as its corresponding patch in A (i.e., they look the same if you squint your eyes), then I also want the same relationship between B and B’. This led to a simple algorithm that generalizes Alyosha’s texture synthesis algorithm, and produced results like this:

I developed this method together with my collaborators Nuria Oliver, Chuck Jacobs, Brian Curless and David Salesin, and we called it Image Analogies, because the algorithm completes the analogy A:A’::B:B’. (Efros and Bill Freeman of MIT also published a closely related texture transfer idea at the same time that we did.)

We could also stylize images where no “source” A was provided, simply by generating A from A’, such as in this example:

We also developed several other applications of the same algorithm. For example, in texture-by-numbers, we can perform texture synthesis in which a user uses the B image to indicate which textures goes where:

This method later served as one of the inspirations for the demos accompanying the PatchMatch algorithm that became Content-Aware Fill in Photoshop.

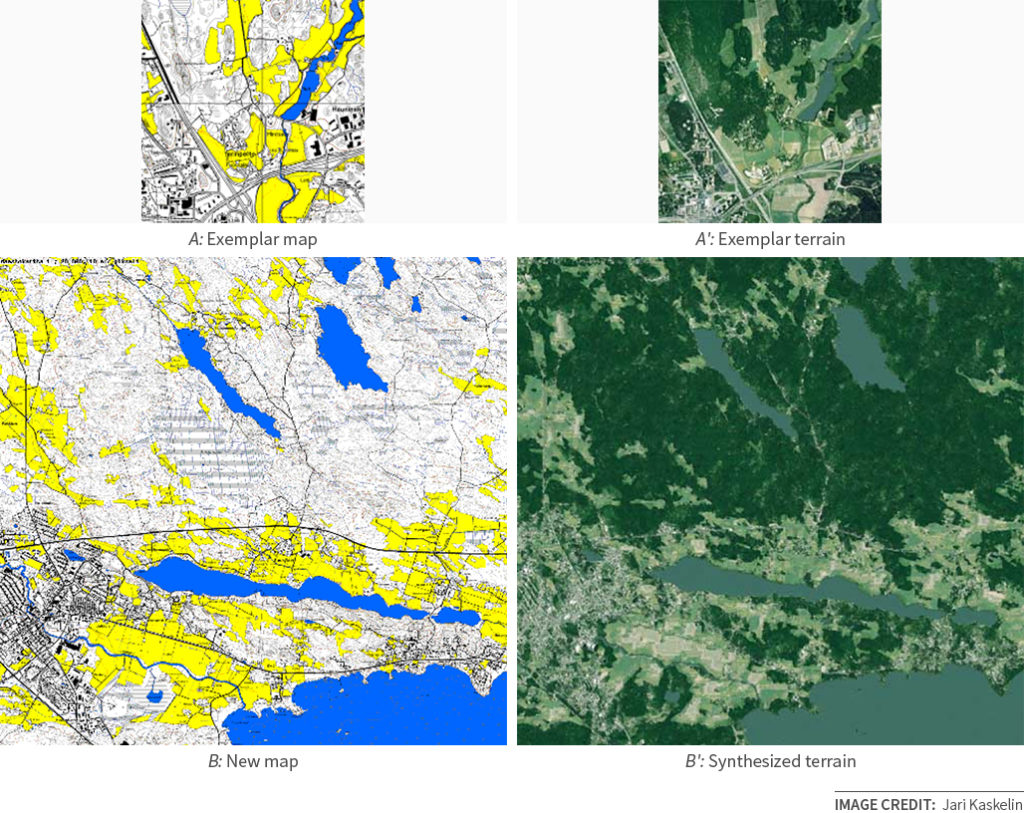
Once I placed the code for this algorithm on the web, people found other uses for it. For example, a fellow named Jari Kaskelin used aerial surveys and maps of Finland to create a method to synthesize satellite imagery from maps, for use in his flight simulator:

Improved Image Analogies: StyLit and Puppetron

Our original Image Analogies algorithm was slow and was very sensitive to variations in input images. For example, it worked well with Van Gogh’s Starry Night on the Rhone (1888), in which most of the stroke textures in the sky are drawn horizontally, whereas it did poorly with Van Gogh’s The Starry Night (1889), in which the sky contains many different textures with different shapes and orientations. Image Analogies was been applied to artist-driven computer animation by a group of researchers at Pixar.

In 2016, a team of researchers from Adobe and Czech Technical University Prague published StyLit, which is now the best Image Analogies algorithm, incorporating ideas from PatchMatch, energy minimization, and their own clever improvements. In this paper, and their follow-up portrait stylization paper, they demonstrate many impressive results:

This method has also be used to develop Puppetron for real-time facial stylization, and is currently in beta in Adobe Character Animator.

In the final post in this series, I’ll describe how neural stylization came along and made stylization wildly popular.

Acknowledgments. Thanks to Alyosha Efros, Eli Schechtman, Eero Simoncelli, and Daniel Sýkora for comments on this post.